|
|
Compressed Sensing for Dynamic PETDynamic positron emission tomography (PET) is widely used to measure changes in the bio-distribution of radiopharmaceuticals within particular organs of interest over time. However, to retain sufficient temporal resolution, photon counts in each time frame should be limited, so conventional reconstruction algorithms such as the ordered subset expectation maximization (OSEM) produce noisy reconstructions. To address this problem, many advanced reconstruction algorithms have been developed using various spatio-temporal regularizations. In this work, we propose a novel spatio-temporal regularization approach that exploits inherent similarities in inter and intra frames. In such correlations, we are interested in a low rank constraint of spatio-temporal patches that is less sensitive to global intensity variations, which is originated from the matrix completion in compressed sensing (CS) theory. To solve non-convex problem, we also provide an optimization method using the concave-convex procedure (CCCP) by exploiting the Legendre-Fenchel transform. We confirm that the proposed algorithm can improve image quality as well as extract accurate kinetic parameters.
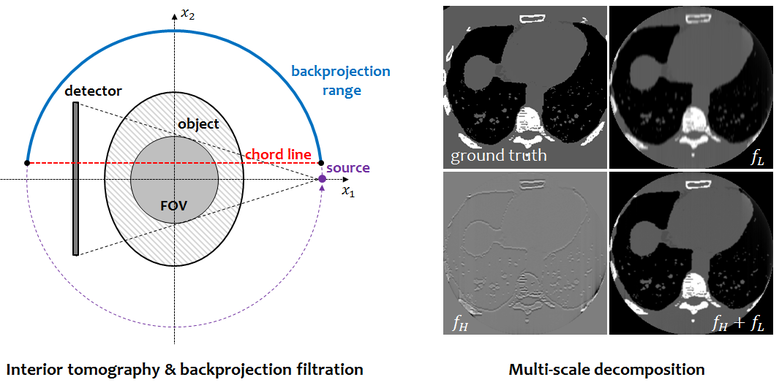
Interior Tomography for X-ray CT In x-ray computed tomography (CT), reconstruction of region of interest (ROI) from local projection data has been called for to reduce radiation exposure in imaging specific organs such as heart, or to reduce size of x-ray detector for cost saving. Using backprojection filtration (BPF) algorithm, after backprojecting the differentiated projection data on chord lines, the original 2D or 3D reconstruction problem is converted into a set of 1D Hilbert filtration problems. If exact differentiated backprojection (DBP) signal on the chord line can cover the whole object, the object can be reconstructed by 1D finite inverse Hilbert transform of DBP along the chord line. But, in interior problems, enough exact DBP signal is not available, so this Hilbert transform relationship needs to be solved by more complicated method. Now, we are trying to find accurate and fast algorithm to solve this truncated Hilbert transform problem using total variation (TV) penalty and multi-scale decomposition, and the simulation result shows the proposed algorithm can produce high quality reconstruction with significantly reduced computational time to practical level even for helical cone-beam CT.
|
|
ABOUT US
Our research activities are primarily focused on the signal processing and machine learning for high-resolution high-sensitivity image reconstruction from real world bio-medical imaging systems. Such problems pose interesting challenges that often lead to investigations of fundamental problems in various branches of physics, mathematics, signal processing, biology, and medicine. While most of the biomedical imaging researchers are interested in addressing this problem using off-the-self tools from signal processing, machine learning, statistics, and optimization and combining their domain-specific knowledge, our approaches are unique in the sense that I believe that actual bio-medical imaging applications are a source of endless inspiration for new mathematical theories and we are eager to solve both specific applications and application-inspired fundamental theoretical problems.
|
CONTACT US
Bio Imaging. Signal Processing & Learning
Graduate School of AI KAIST 291 Daehak-ro, Yuseong-gu Daejeon 305-701, Korea Copyright (c) 2014, BISPL All Rights Reserved. |
|