|
|
Compressive MUSICCS-MUSIC
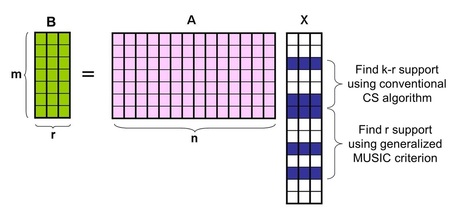
The multiple measurement vector (MMV) problem addresses the identification of unknown input vectors that share common sparse support. Even though MMV problems have been traditionally addressed within the context of sensor array signal processing, the recent trend is to apply compressive sensing (CS) due to its capability to estimate sparse support even with an insufficient number of snapshots, in which case classical array signal processing fails. However, CS guarantees the accurate recovery in a probabilistic manner, which often shows inferior performance in the regime where the traditional array signal processing approaches succeed. The apparent dichotomy between the probabilistic CS and deterministic sensor array signal processing has not been fully understood. Recently, we developed a unified approach that unveils a missing link between CS and array signal processing. The new algorithm, which we call compressive MUSIC, identifies the parts of support using CS, after which the remaining supports are estimated using a novel generalized MUSIC criterion. Using a large system MMV model, we show that our compressive MUSIC requires a smaller number of sensor elements for accurate support recovery than the existing CS methods and that it can approach the optimal L0-bound with finite number of snapshots. Sequential CS-MUSIC
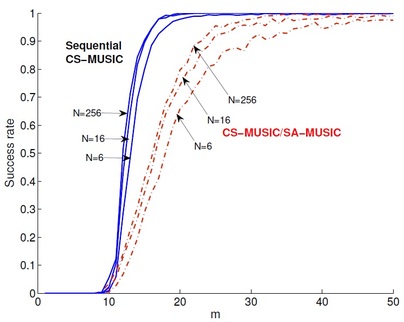
In a multiple measurement vector problem (MMV), where multiple signals share a common sparse support and are sampled by a common sensing matrix, we can expect joint sparsity to enable a further reduction in the number of required measurements. While a diversity gain from joint sparsity had been demonstrated earlier in the case of a convex relaxation method using an l1/l2 mixed norm penalty, only recently was it shown that similar diversity gain can be achieved by greedy algorithms if we combine greedy steps with a MUSIClike subspace criterion. However, the main limitation of these hybrid algorithms is that they often require a large number of snapshots or a high signal-to-noise ratio (SNR) for an accurate subspace as well as partial support estimation. One of the main contributions of this work is to show that the noise robustness of these algorithms can be significantly improved by allowing sequential subspace estimation and support filtering, even when the number of snapshots is insufficient. Numerical simulations show that a novel sequential compressive MUSIC (sequential CS-MUSIC) that combines the sequential subspace estimation and support filtering steps significantly outperforms the existing greedy algorithms and is quite comparable with computationally expensive state-of-art algorithms.
Software Requirements MATLAB (Mathworks, Natick, MA, http://www.mathworks.com).
Acknowledgement This research was supported by the Korea Science and Engineering Foundation (KOSEF) grant funded by the Korea government (MEST) (No.2011-0000353). Copyright (c) 2011, Jong Min Kim, Ok Kyun Lee and Jong Chul Ye, KAIST Joint sparse recovery package is free; you can distribute it and/ or modify it under the terms of the GNU General Public License (GPL) as publishing by the Free Software Foundation, either version 3 of the License, or any later version. For the copy of the GNU General Public License, see (http://www.gnu.org/licenses/). Additional Note from Authors You can get the software freely - including source code - by downloading it here. We appreciate if you cite the following papers in producing the results using joint sparse recovery package. [1] J. M. Kim, O. K. Lee, and J. C. Ye, Compressive MUSIC: Revisiting the Link Between Compressive Sensing and Array Signal Processing. IEEE Trans. Inf. Theory, vol. 58, no. 1, pp. 278-301, Jan 2012. [2] J. M. Kim, O. K. Lee, and J. C. Ye, Compressive MUSIC with optimized partial support for joint sparse recovery. in Proc. IEEE Int. Symp. Inf. Theory (ISIT), 2011. [3] J. M. Kim, O. K. Lee, and J. C. Ye, Improving Noise Robustness in Subspace-based Joint Sparse Recovery. IEEE Trans. Signal Process, vol. 60, no. 11, pp. 5799-5809, Nov 2012. Copyright (c) 2012, Jong Chul Ye.
|
|
ABOUT US
Our research activities are primarily focused on the signal processing and machine learning for high-resolution high-sensitivity image reconstruction from real world bio-medical imaging systems. Such problems pose interesting challenges that often lead to investigations of fundamental problems in various branches of physics, mathematics, signal processing, biology, and medicine. While most of the biomedical imaging researchers are interested in addressing this problem using off-the-self tools from signal processing, machine learning, statistics, and optimization and combining their domain-specific knowledge, our approaches are unique in the sense that I believe that actual bio-medical imaging applications are a source of endless inspiration for new mathematical theories and we are eager to solve both specific applications and application-inspired fundamental theoretical problems.
|
CONTACT US
Bio Imaging. Signal Processing & Learning
Graduate School of AI KAIST 291 Daehak-ro, Yuseong-gu Daejeon 305-701, Korea Copyright (c) 2014, BISPL All Rights Reserved. |
|